Opposite category

In category theory, a branch of mathematics, the opposite category or dual category C^op of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite category is the original category itself. In symbols, .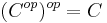

Contents 1 Examples 2 Properties 3 References 4 See also

Examples

• An example comes from reversing the direction of inequalities in a partial order. So if X is a set and ≤ a partial order relation, we can define a new partial order relation ≤_new by

x ≤_new y if and only if y ≤ x.

For example, there are opposite pairs child/parent, or descendant/ancestor.

• The category of Boolean algebras and Boolean homomorphisms is equivalent to the opposite of the category of Stone spaces and continuous functions.

• The category of affine schemes is equivalent to the opposite of the category of commutative rings.

• The Pontryagin duality restricts to an equivalence between the category of compact Hausdorff abelian topological groups and the opposite of the category of (discrete) abelian groups.

• By the Gelfand-Neumark theorem, the category of localizable measurable spaces (with measurable maps) is equivalent to the category of commutative Von Neumann algebras (with normal unital homomorphisms of *-algebras).^[1]

Properties

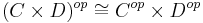(see product category)

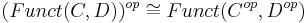^[2][3] (see functor category)

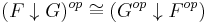(see comma category)

References

See also

• Dual object
• Dual (category theory)
• Duality (mathematics)
• Contravariant functor
• Opposite functor

Citations